This is a project, that I used to play around with Linear Algebra and command-line ANSI printing in Rust. The result is a 3D cube, spinning in an arbitrary direction, with a soft see through factor. You can find the code on my Github, here.
The Linear Algebra behind it all
The most interesting part in this project is the Linear Algebra ofcourse which makes it all work.
“A basic rotation (also called elemental rotation) is a rotation about one of the axes of a coordinate system. The following three basic rotation matrices rotate vectors by an angle θ about the x-, y-, or z-axis, in three dimensions, using the right-hand rule—which codifies their alternating signs.” ~ Swokowski, Earl (1979)
Knowing this, and playing around with cos and sin in a three dimensional matrix, we can formulate the following three matrices:

Let’s consider the rotation angles as follows: θx for the roll, θy for the pitch, and θz for the yaw.
The combined rotation matrix (x-axis, y-axis, z-axis) can be obtained by multiplying the individual rotation matrices in the desired order:
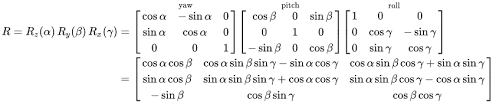
In this combined rotation matrix, the values of cos(θx), cos(θy), and cos(θz) represent the cosine values of the roll, pitch, and yaw angles, respectively. Similarly, sin(θx), sin(θy), and sin(θz) represent the sine values of the roll, pitch, and yaw angles, respectively.
Please substitute the desired rotation angles (θx, θy, θz) with the specific values you want to achieve the corresponding combined rotation matrix for your application.
Using this piece of Linear Algebra, I was able to code it up in Rust and get the result as displayed above!